በሂሳብ ውስጥ ማጠቃለያ (በትልቁ የግሪክ ሲግማ ምልክት የተገለፀው) የቁጥሮች ማጠቃለያ ነው። መጠኑ ስንት ነው? ይህ የእንደዚህ አይነት ድርጊት ውጤት ነው. ቁጥሮቹ ከግራ ወደ ቀኝ አንድ በአንድ ከተጨመሩ፣ መካከለኛው ውጤት ከፊል ድምር ነው።
መጠኑ ስንት ነው?
የሚደመሩ ቁጥሮች ኢንቲጀር፣ ምክንያታዊ፣ እውነተኛ ወይም ውስብስብ ሊሆኑ ይችላሉ። ከነሱ በተጨማሪ ሌሎች የእሴቶች ዓይነቶች ሊጨመሩ ይችላሉ፡- ቬክተር፣ ማትሪክስ፣ ፖሊኖሚሎች እና በአጠቃላይ የማንኛውም ተጨማሪ ቡድን (ወይም ሞኖይድ)።
የቃላቱ ንጥረ ነገሮች ብዛት ካለቀ፣ማጠቃለያው ሁል ጊዜ በደንብ የተገለጸ ዋጋ ይሰጣል። ማለቂያ የሌለው የእሴቶች ማጠቃለያ ተከታታይ ይባላል። እሴቱ ብዙውን ጊዜ ገደብ በመጠቀም ሊታወቅ ይችላል (ምንም እንኳን አንዳንድ ጊዜ እሴቱ ማለቂያ የሌለው ሊሆን ይችላል)።
ተከታታዮች
የቁጥሮች ማጠቃለያ [3፣7፣2፣1] እሴቱ በውስጡ የተካተቱት የአሃዞች ድምር በሆነ አገላለጽ ሊገለጽ ይችላል ለምሳሌ 3 + 7 + 2 + 1=13. መደመርበማያያዝ፣ ድምሩ ቃላቶቹ እንዴት እንደተከፋፈሉ ላይ የተመካ አይደለም፣ ለምሳሌ (3+7)+ (2+1) እና 3+ ((7+2)+1) ሁለቱም ከዘጠኝ ጋር እኩል ናቸው፣ ስለዚህ ቅንፍ አብዛኛውን ጊዜ ነው። ጋር ተከፋፍሏል. መደመር እንዲሁ ተለዋጭ ነው፣ ስለዚህ ቃላቶቹን እንደገና ማስተካከል የድምሩ ዋጋ አይለውጠውም። ይህ ንብረት ላልተወሰነ ማጠቃለያ ላይሰራ እንደሚችል ልብ ይበሉ።

የእንደዚህ አይነት ቅደም ተከተሎችን ለማጠቃለል ምንም ልዩ ምልክት የለም። ከሁለት ያነሱ ንጥረ ነገሮች ካሉ ትንሽ ትንሽ ነገር ብቻ ነው. የአንድ አባል ቅደም ተከተል ማጠቃለያ የመደመር ምልክት አልያዘም (ከቁጥሩ መልክ አይለይም) እና ምንም ንጥረ ነገሮች ከሌሉ እንኳን ሊፃፍ አይችልም (ነገር ግን ይልቁንስ በ ሊያመለክት ይችላል) የእሱ ዋጋ "0"). ይሁን እንጂ የቅደም ተከተል ቃላቶቹ በተወሰነ ስርዓተ-ጥለት ከተገለጹ፣ ለምሳሌ ተግባር፣ ከዚያም የማጠቃለያ ኦፕሬተሩ ጠቃሚ ወይም አስፈላጊ ሊሆን ይችላል።
መቅረጽ
አንድ ድምር ምን እንደሆነ ለመረዳት እንዲሁ መልኩን መተንተን ያስፈልጋል።
ከ1 እስከ 100 ያለውን ተከታታይ ኢንቲጀር ለማጠቃለል፣ የጎደሉትን አባላት ለማመልከት ኤሊፕሲስን የሚያካትት አገላለጽ ብዙ ጊዜ ጥቅም ላይ ይውላል፡ 1 + 2 + 3 + 4 + … + 99 + 100። በዚህ ምሳሌ ውስጥ በቀላሉ ለማየት. ነገር ግን, ለተጨማሪ ውስብስብ አማራጮች, የ "Σ" ማጠቃለያ ኦፕሬተርን በመጠቀም ሊገኝ የሚችለውን የንጥሎች ዋጋ ለማግኘት ጥቅም ላይ የዋለውን ደንብ በትክክል መግለጽ አስፈላጊ ነው. ይህን ምልክት (ሲግማ) በመጠቀም የሚከተለውን ምልክት መተግበር ይችላሉ፡
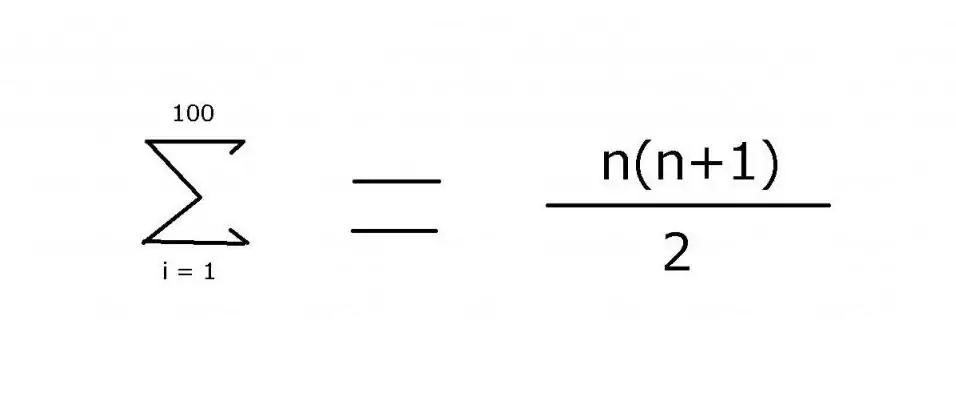
የዚህ አገላለጽ ዋጋ 5050 ነው።በሂሳብ ኢንዳክሽን በመጠቀም ሊገኝ ይችላል ይህም የቀመርው ሁለተኛ ክፍል የመጣበት ነው።
ለተለያዩ ቅደም ተከተሎች፣ ቀመሩ ይቀየራል። የመቅዳት ሂደቱ የአንዳንድ ማለቂያ የለሽ ቅደም ተከተሎችን ቅድመ-ምስል ለመፈለግ እና ከዚያም በቀመር ወደ መግለጽ ይቀንሳል። ይህን ካደረግኩ በኋላ፣ በአንድ የተወሰነ ጉዳይ ላይ መጠኑ ምን እንደሆነ ለመረዳት አስቸጋሪ አይደለም።
ቁጥሮች ከመልክቶቻቸው (ሲደመር ወይም ሲቀነስ) መጨመሩን ግልጽ ለማድረግ ሲያስፈልግ፣ አልጀብራ ድምር የሚለው ቃል ጥቅም ላይ ይውላል። ለምሳሌ በኤሌክትሪካል ሰርክዩር ቲዎሪ የኪርቾፍ ወረዳ ህጎች በአንድ ነጥብ ላይ በተገናኙት የኦርኬስትራ ኔትዎርክ ውስጥ ያለውን የወቅቱን አልጀብራ ድምር ግምት ውስጥ በማስገባት በመስቀለኛ መንገድ ውስጥ ለሚፈሱ ጅረቶች ተቃራኒ ምልክቶችን ይሰጣሉ።






