የኤሌክትሪክ ዲፖል። ፊዚክስ ፣ 10 ኛ ክፍል። ኤሌክትሮዳይናሚክስ

2024 ደራሲ ደራሲ: Angel Austin | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2024-01-02 17:40

ፊዚክስን በ10ኛ ክፍል ስታጠና የዲፕሎልስ ርዕስ ግምት ውስጥ ይገባል። ይህ ጽንሰ-ሐሳብ ምን ማለት ነው እና እሱን ለማስላት ምን ቀመሮች ጥቅም ላይ ይውላሉ?

መግቢያ

አንድ ዳይፖል ወጥ በሆነ የኤሌትሪክ መስክ ቦታ ላይ ካስቀመጡት እንደ ሃይል መስመሮች ሊወክሉት ይችላሉ። ዲፕሎል በመለኪያዎች ተመሳሳይነት ያላቸው ሁለት ክፍያዎች ያሉበት ስርዓት ነው ፣ ግን እነሱ ተቃራኒ የነጥብ ክፍያዎች ናቸው። ከዚህም በላይ በመካከላቸው ያለው ርቀት ከየትኛውም የዲፕላስ መስክ ርቀት በጣም ያነሰ ይሆናል. የዲፕሎል አፍታ ጽንሰ-ሀሳብ በትምህርት ቤት የኤሌክትሮዳይናሚክስ ኮርስ (10ኛ ክፍል) ውስጥ ተጠንቷል።

የዲፖል ዘንግ በሁለቱም ቻርጆች ነጥቦች ውስጥ የሚያልፍ ቀጥተኛ መስመር ነው። ዲፕሎል ክንድ ክፍያን የሚያገናኝ ቬክተር ሲሆን በተመሳሳይ ጊዜ ከአሉታዊ ቻርጅ ወደ አወንታዊ ቻርጅ ቅንጣቶች ይሄዳል። የኤሌትሪክ ዲፖል የሚታወቀው እንደ ዲፖል ወይም ኤሌትሪክ ቅጽበት ያለ ሁኔታ በመኖሩ ነው።

በትርጓሜ፣ የዲፖል አፍታ ከዲፖል ቻርጅ እና ክንዱ ጋር በቁጥር እኩል የሆነ ቬክተር ነው። ከዚህም በላይ ከዲፕላስ ትከሻ ጋር አብሮ ይመራል. የኃይላት ድምር ዜሮ እኩልነት፣ የወቅቱን ዋጋ እናሰላለን። በዲፕሎል ቅፅበት እና መካከል ለሚኖረው አንግልየኤሌክትሪክ መስክ አቅጣጫ, የሜካኒካል አፍታ መገኘት ባህሪይ ነው.

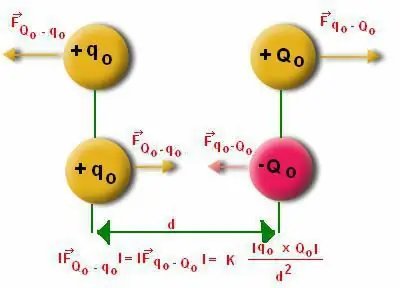
ብዙውን ጊዜ ሰዎች በዲፕሎል መዋቅር ላይ የሚሰራውን ሞጁል ለማስላት ይቸገራሉ። እዚህ ላይ "አልፋ" የሚለውን አንግል ለማስላት ልዩ ባህሪያትን ግምት ውስጥ ማስገባት ያስፈልጋል. ዲፖሉ ከተመጣጣኝ ቦታ እንደሚለይ ይታወቃል. ነገር ግን የመንቀሳቀስ አዝማሚያ ስላለው የዲፕሎል አፍታ ራሱ ወደነበረበት የሚመለስ ገጸ ባህሪ አለው።

ስሌቶች

ይህ የዲፕሎፕ አፍታ ተመሳሳይነት በሌለው የኤሌትሪክ መስክ መካከለኛ ውስጥ ሲገባ፣ ኃይል መፈጠሩ የማይቀር ነው። በእንደዚህ ዓይነት አከባቢ ውስጥ የኃይሎች ድምር ጠቋሚዎች ዜሮ አይሆኑም. ስለዚህ፣ በዲፕሎል ቅፅበት ላይ የነጥብ ቁምፊ ያላቸው ኃይሎች አሉ። የዲፖል ክንድ መጠን በጣም ትንሽ ነው።

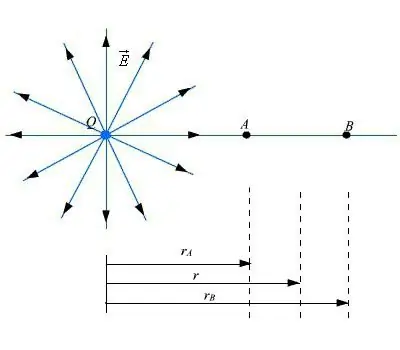
ቀመሩ እንደሚከተለው ሊፃፍ ይችላል፡ F=q (E2 - E1)=qdE፣መ የኤሌትሪክ መስክ ልዩነት ነው።

በጥናት ላይ ያለውን የአካላዊ ጽንሰ-ሀሳብ ባህሪያትን ይፈልጉ

እስቲ ርዕሱን የበለጠ እንመልከተው። የኤሌክትሪክ መስክ ባህሪው ምን እንደሆነ ለመወሰን, የክፍያ ስርዓትን በመጠቀም ከተፈጠረ እና በትንሽ ቦታ ውስጥ አካባቢያዊ ከሆነ, በርካታ ስሌቶችን ማድረግ አስፈላጊ ነው. ለምሳሌ በአተሞች እና ሞለኪውሎች ቀርቧል፣በነሱ አቀነባበር በኤሌክትሪክ የተሞሉ ኒዩክሊይ እና ኤሌክትሮኖች አሉ።

በእርቀቱ ቦታን ለመፈለግ አስፈላጊ ከሆነ ቅንጣቶች የሚገኙበትን ቦታ ከሚፈጥሩት ልኬቶች በላይ በሆነ ርቀት ላይ, በጣም ውስብስብ የሆኑ በርካታ ትክክለኛ ቀመሮችን እንጠቀማለን. ቀለል ያለ መጠቀም ይቻላልግምታዊ መግለጫዎች. የነጥብ ስብስቦች q_{k በኤሌክትሪክ መስክ መፍጠር ላይ ይሳተፋሉ ብለን እናስብ። በትንሽ ቦታ ላይ ይገኛሉ።}

መስኩ ያለውን ባህሪ ለማስላት ሁሉንም የስርዓቱን ክፍያዎች ማዋሃድ ይፈቀድለታል። እንዲህ ዓይነቱ ሥርዓት እንደ ነጥብ ክፍያ ይቆጠራል Q. የመጠን አመልካቾች በዋናው ሥርዓት ውስጥ የነበሩት ክፍያዎች ድምር ይሆናሉ።

የክፍያዎች መገኛ

የክፍያው መገኛ q_{k የሚገኝበት በማንኛውም ቦታ ላይ እንደሆነ እናስብ። በቦታው ላይ ለውጦችን በሚያደርጉበት ጊዜ, በትንሽ ቦታ ላይ የተገለጹ ገደቦች ካሉት, እንዲህ ዓይነቱ ተጽእኖ በእይታ ውስጥ በሜዳው ላይ ሊደረስ የማይችል, ቸልተኛ ይሆናል. የኤሌክትሪክ መስክ ካለው የጥንካሬ እና እምቅ ግምታዊ ገደቦች ውስጥ፣ ተለምዷዊ ቀመሮችን በመጠቀም ይወሰናል።}

የስርዓቱ አጠቃላይ ክፍያ ድምር ዜሮ ሲሆን የተጠቆመው የተጠጋጋ መለኪያዎች ሸካራ ይሆናሉ። ይህ የኤሌክትሪክ መስክ በቀላሉ የለም ብሎ ለመደምደም ምክንያት ይሰጣል. ይበልጥ ትክክለኛ የሆነ ግምት ለማግኘት አስፈላጊ ከሆነ፣ ከግምት ውስጥ የሚገቡትን የስርዓቱን አወንታዊ እና አሉታዊ ክፍያዎች በአእምሯዊ ሁኔታ ይሰብስቡ።

የእነርሱ "ማዕከሎች" ከሌሎች ጋር ሲፈናቀሉ, በእንደዚህ አይነት ስርዓት ውስጥ ያሉ የመስክ መለኪያዎች ሁለት ነጥብ ክፍያዎች ያሉት መስክ ተብሎ ሊገለጽ ይችላል, በመጠን እኩል እና በተቃራኒው ምልክት. ከሌሎች ጋር በተያያዘ መፈናቀላቸውም ተጠቅሷል። ለማቅረብለክፍያዎች ስርዓት የበለጠ ትክክለኛ ባህሪ ከዚህ ግምታዊ ግቤቶች አንፃር ፣ በኤሌክትሪክ መስክ ውስጥ የዲፕሎል ባህሪዎችን ማጥናት አስፈላጊ ነው።

የቃሉ መግቢያ

ወደ ትርጉሙ እንመለስ። ኤሌክትሪክ ዲፖል ሁለት ነጥብ ክፍያዎች ያለው ሥርዓት ፍቺ ነው. ተመሳሳይ መጠን እና ተቃራኒ ምልክቶች አሏቸው. በተጨማሪም፣ እንደዚህ አይነት ምልክቶች ከሌሎች ምልክቶች አንጻር በትንሽ ርቀት ላይ ይገኛሉ።

በዲፕሎል አማካኝነት የሚፈጠረውን የሂደቱን ባህሪ ማስላት ይችላሉ እና በሁለት ነጥብ ክፍያዎች የተወከለው +q እና −q እና ከሌሎቹ አንፃር በሩቅ ይገኛሉ።

የሂሳብ ቅደም ተከተል

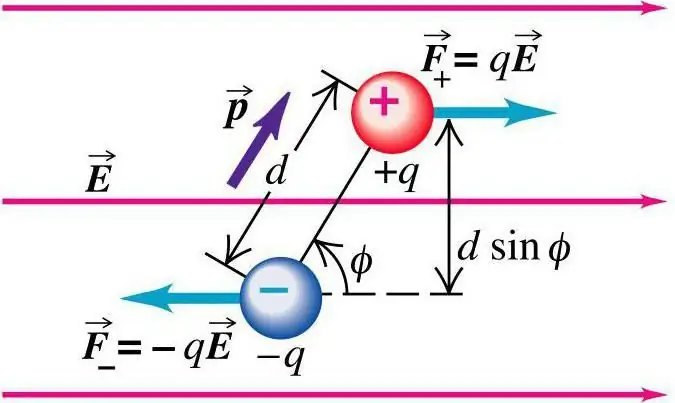
ዲፖሉ በዘንባባው ወለል ላይ ያለውን እምቅ እና ጥንካሬ በማስላት እንጀምር። ይህ በሁለት ክፍያዎች መካከል የሚሄድ ቀጥተኛ መስመር ነው. ነጥብ ሀ ከዲፕሎል ማዕከላዊ ክፍል ጋር እኩል በሆነ ርቀት ላይ የሚገኝ ከሆነ እና r >> a ከሆነ በዚህ ነጥብ ላይ የመስክ አቅም በሱፐርፖዚሽን መርህ መሰረት, ምክንያታዊ ይሆናል. የኤሌትሪክ ዲፖል መለኪያዎችን ለማስላት አገላለጹን ይጠቀሙ።

የጥንካሬ ቬክተር መጠን በሱፐርላይዝድ መርህ ይሰላል።የመስክ ጥንካሬን ለማስላት የችሎታ እና የመስክ ጥንካሬ ጥምርታ ጽንሰ-ሀሳብ ጥቅም ላይ ይውላል፡

ኢ_{x=-Δφ /Δx.}

በእንደዚህ ዓይነት ሁኔታዎች ውስጥ የኃይለኛው ቬክተር አቅጣጫ ከዲፕሎል ዘንግ አንፃር በቁመት ይገለጻል። ሞጁሉን ለማስላት መደበኛው ቀመር ተግባራዊ ይሆናል።

አስፈላጊማብራሪያዎች

የኤሌክትሪክ ዳይፖል መስክ መዳከም የነጥብ ክፍያን ከማግኘት በበለጠ ፍጥነት እንደሚከሰት ግምት ውስጥ ማስገባት ያስፈልጋል። የዲፖል መስክ እምቅ መበስበስ ከርቀት ካሬው ጋር የተገላቢጦሽ ነው, እና የመስክ ጥንካሬ ከርቀት ኪዩብ ጋር ይዛመዳል.

ተመሳሳይ ነገር ግን ይበልጥ አስቸጋሪ የሆኑ ዘዴዎችን በመጠቀም የዲፖሉ እምቅ አቅም እና የመስክ ጥንካሬ መለኪያዎች በዘፈቀደ ነጥቦች ላይ ይገኛሉ ፣የቦታው መለኪያዎች የሚወሰኑት እንደዚህ ባለው ስሌት ዘዴ እንደ የዋልታ መጋጠሚያዎች ነው-ለ የኤሌትሪክ ዲፖል መሃል (r) እና አንግል (θ)።

የጭንቀት ቬክተር በመጠቀም ስሌት

የኃይለኛነት ቬክተር ኢ ጽንሰ-ሐሳብ በሁለት ነጥቦች ይከፈላል፡

• Radial (E_{r)፣ እሱም ከቀጥታ መስመር አንጻር ወደ ቁመታዊ አቅጣጫ የሚመራ።}
• እንዲህ ዓይነቱ ቀጥተኛ መስመር የተገለጸውን ነጥብ እና የዲፕሎሉን መሃከል ከቋሚው ጋር ያገናኛል E_θ።

ይህ የእያንዳንዱ አካል መበስበስ የሚመራው በሁሉም የነጥብ መጋጠሚያዎች በሚፈጠረው የለውጥ ሂደት ነው። የመስክ ጥንካሬ አመልካቾችን እና ሊሻሻሉ የሚችሉ ማሻሻያዎችን በሚያገናኘው ጥምርታ ሊያገኙት ይችላሉ።

የቬክተር ክፍላትን በመስክ ጥንካሬ ለማግኘት፣ የእይታ ነጥቡ ወደ ቬክተር አቅጣጫ በመፈናቀሉ ምክንያት ሊከሰቱ በሚችሉ ለውጦች የግንኙነቱን ባህሪ ማረጋገጥ አስፈላጊ ነው።

የቋሚውን ክፍል አስላ

ሲጠናቀቅለዚህ አሰራር በትንሽ ቋሚ ማፈናቀል ላይ ያለውን የመለኪያ አገላለጽ አንግል በመለወጥ እንደሚወሰን ግምት ውስጥ ማስገባት አስፈላጊ ነው-Δl=rΔθ. የዚህ የመስክ ክፍል መጠን መለኪያዎች እኩል ይሆናሉ.

ጥምርታውን ካገኘ በኋላ በዚህ መስክ የሃይል መስመሮች ምስል ለመገንባት የኤሌክትሪክ ዲፖሉን መስክ በዘፈቀደ ነጥብ መወሰን ይቻላል ።

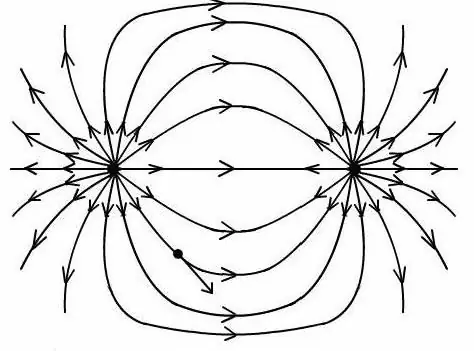
የዲፕሎል አቅም እና የመስክ ጥንካሬን ለመወሰን ሁሉም ቀመሮች የሚሰሩት አንድ ዲፕሎል ቻርጅ ባላቸው እሴቶች እና በመካከላቸው ባለው ርቀት ላይ ብቻ መሆኑን ግምት ውስጥ ማስገባት አስፈላጊ ነው።

Dipole moment

የተገለፀው ስራ ርዕስ ስለ ኤሌክትሪክ አይነት ሙሉ መግለጫ ነው። እሱ "የስርዓቱ ዳይፖል አፍታ" የሚል ስም አለው።

በዲፖል ፍቺ የነጥብ ክፍያዎች ሥርዓት በሆነው የአክሱም ሲሜትሪ ተለይቶ የሚታወቅ ሲሆን ዘንግው በበርካታ ክፍያዎች ውስጥ የሚያልፍ ቀጥተኛ መስመር ነው።

የዲፕሎሉን ሙሉ ባህሪ ለማዘጋጀት ዘንግ ያለውን የአቅጣጫ አቅጣጫ ያመልክቱ። ለስሌቶች ቀላልነት, የዲፕሎል አፍታ ቬክተር ሊገለጽ ይችላል. የክብደቱ ዋጋ ከዲፕሎል ቅፅበት መጠን ጋር እኩል ነው, እና የአቅጣጫው ቬክተር በእሱ እና በዲፕል ዘንግ ላይ በአጋጣሚ ይለያያል. ስለዚህ p=qa a የዲፕሎሉን አሉታዊ እና አወንታዊ ክፍያዎች የሚያገናኘው የቬክተር አቅጣጫ ከሆነ።

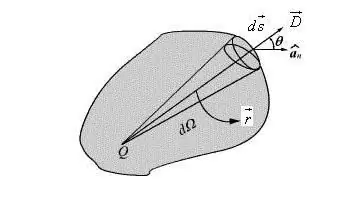
እንዲህ አይነት የዲፕሎል ባህሪን መጠቀም ምቹ እና በአብዛኛዎቹ ሁኔታዎች ቀመሩን ለማቃለል እና ቅጹን ለመስጠት ያስችላል።ቬክተር. በዘፈቀደ አቅጣጫ ያለው የዲፖል መስክ አቅም መግለጫው በቬክተር መልክ ተጽፏል።

እንደ ዲፖል የቬክተር ባህሪ እና የዲፕሎል አፍታ ያሉ ጽንሰ-ሀሳቦችን ማስተዋወቅ ቀለል ባለ ሞዴል - የነጥብ ክፍያ በአንድ ወጥ መስክ ውስጥ ሊከናወን ይችላል ፣ ይህም የክፍያ ስርዓትን ያጠቃልላል ፣ የጂኦሜትሪክ ልኬቶች ግምት ውስጥ መግባት የለበትም, ነገር ግን የዲፕሎል አፍታውን ማወቅ አስፈላጊ ነው. ስሌቶችን ለማከናወን ይህ ቅድመ ሁኔታ ነው።

ዲፖል እንዴት እንደሚሠራ

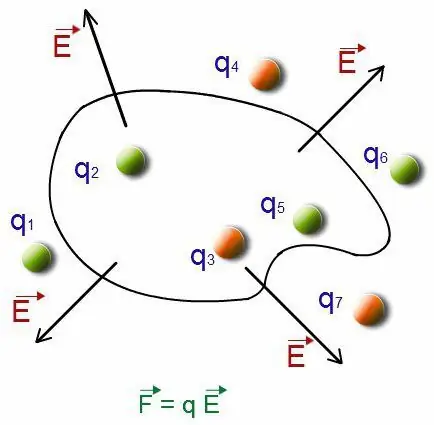
የዲፕሎል ባህሪ በዚህ ሁኔታ ምሳሌ ላይ ሊታይ ይችላል። የሁለት ነጥብ ክፍያዎች አቀማመጥ አንዳቸው ከሌላው አንጻር የርቀት ቋሚ ባህሪ አላቸው. አንድ ወጥ የሆነ የኤሌክትሪክ መስክ በዲፕሎል ሁኔታዎች ውስጥ ተቀምጠዋል. በሂደቱ ላይ ምልከታ አድርጓል። በፊዚክስ (ኤሌክትሮዳይናሚክስ) ትምህርቶች, ይህ ጽንሰ-ሐሳብ በዝርዝር ይታያል. ከሜዳው እስከ ክፍያው ድረስ የኃይሎች እርምጃ ይከናወናል፡

F=±qE

በመጠን እና በአቅጣጫ ተቃራኒ ናቸው። በዲፕሎል ላይ የሚሠራው አጠቃላይ ኃይል ጠቋሚው ዜሮ ነው. እንዲህ ዓይነቱ ኃይል በተለያዩ ነጥቦች ላይ ተጽእኖ ስለሚያሳድር አጠቃላይ ጊዜው የሚከተለው ይሆናል፡-

M=Fa sin a=qEa sin a=pE sin a

ከ α ጋር የመስክ ጥንካሬ ቬክተሮችን እና የዲፖል ቅጽበት ቬክተሮችን የሚያገናኝ አንግል ነው። የኃይል አፍታ በመኖሩ ምክንያት የስርዓቱ የዲፕሎል ቅጽበት ወደ ኤሌክትሪክ መስክ ጥንካሬ ቬክተር አቅጣጫዎች የመመለስ አዝማሚያ ይኖረዋል።

የኤሌክትሪክ ዲፖል በግልፅ ለመረዳት አስፈላጊ የሆነ ፅንሰ-ሀሳብ ነው። በይነመረብ ላይ ስለ እሱ የበለጠ ማንበብ ይችላሉ። ደግሞም ይችላል።ከላይ እንደተናገርነው በትምህርት ቤት በፊዚክስ ትምህርት ለመማር 10ኛ ክፍል።