ተማሪዎቹ ባደጉ ቁጥር ቀላል ችግሮችን ለመፍታት የፍጥነት ፍላጎት እየጨመረ ይሄዳል። ቀላል ምሳሌዎችን ወይም ችግሮችን ለረጅም ጊዜ ለመፍታት በፈተናዎች ውስጥ ብዙ ጊዜ አይሰጥም. የካሬውን ዲያግናል በፍጥነት እና በቀላሉ እንዴት ማግኘት ይቻላል? ይህ ከስምንተኛ ክፍል ላሉ ልጆች ይማራል። ይህ መጣጥፍ ሁለት መንገዶችን ያሳያል - አንዱ ይረዝማል፣ ሌላኛው ፈጣን ነው።
የካሬውን ሰያፍ እንዴት ማስላት ይቻላል?
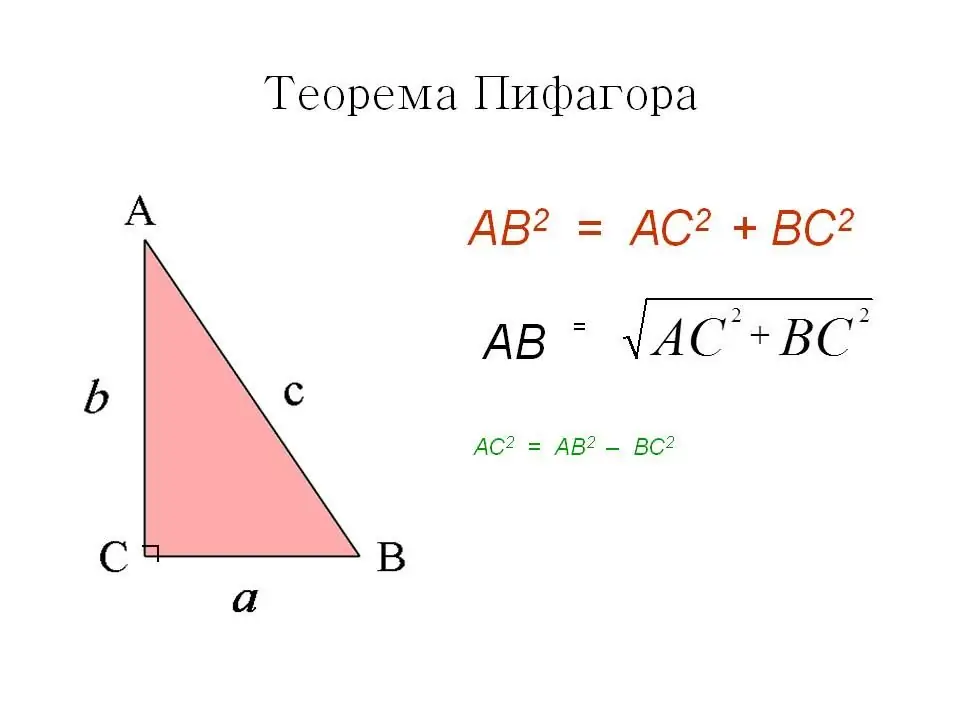
የመጀመሪያው መንገድ የታወቀው እና የተለመደው የፓይታጎሪያን ቲዎሪ ነው። በካሬው ውስጥ, ሁሉም ማዕዘኖች ትክክል ናቸው, ይህም ማለት ዲያግኖል ወደ ሁለት እኩል የቀኝ ማዕዘን ትሪያንግሎች ይከፍላል እና እራሱ hypotenuse ነው. እንደ ፓይታጎሪያን ቲዎሬም ፣ የ hypotenuse ካሬ ከእግሮቹ ካሬዎች ድምር ጋር እኩል ነው።

ሁለተኛው መንገድ ለካሬዎች ልዩ የሆነ ቀላል ቀመር ነው እና እሱን ማስታወስ ብቻ ያስፈልግዎታል። እንደሚታወቀው የአንድ ካሬ ሁሉም ጎኖች እኩል ናቸው ለዚህም ነው የሒሳብ ሊቃውንት ዲያግናልን ለማግኘት የሚከተለውን ቀመር ያሰሉት፡ ከጎኑ እና የሁለት ሥሩ እኩል ነው።
በእርግጥ የአንድ ካሬ ሰያፍ ርዝመት ያለውን ቀመር ብቻ ማስታወስ እና ሁልጊዜም መጠቀም ጥሩ ነው ምክንያቱም በጣም ፈጣን እና ምቹ ነው። ይህ በተለይ የሚሰማው ችግሮችን በጥሬው ሲፈታ ነው፡ ከትላልቅ ስርወ መግለጫዎች ይልቅ በአንድ ምርት ብቻ ማግኘት ይችላሉ።
ምሳሌ
ለምሳሌ 6 በ 6 ካሬ ማለትም ጎን ስድስት ሴንቲሜትር የሚያህል ጎን ይውሰዱ።
በመጀመሪያው ዘዴ መሰረት፡ ዲያግናል ሐ ይሁን፣ እና ጎኑ A. ይሁን።
ከዚያም ያንን C=√A^2+A^2 ወይም C=√2A^2 እናገኛለን።
በቁጥር እንጽፈው፡ С=√36 + 36. √72 አግኝተናል ይህም 3√8 ወይም 6√2 ነው። አግኝተናል።
እና አሁን አንድ አይነት ሰያፍ እናገኝ፣ነገር ግን በሁለተኛው ዘዴ፡C=A√2 ወይም በቁጥር፡6√2
አሁን ሁለተኛው ዘዴ ምን ያህል ፈጣን፣ቀላል እና ከሁሉም በላይ አስፈላጊ እንደሆነ ማየት ይችላሉ - የበለጠ ቀልጣፋ በተለይም እንደዚህ ባሉ ቀላል ችግሮች ውስጥ እያንዳንዱ ደቂቃ በፈተና ውድ ናት!
ሌሎች የካሬ ሰያፍ ባህሪያት
የካሬውን ዲያግራናሎች እንዴት ማግኘት እንደሚችሉ ከማወቅ በተጨማሪ ንብረታቸውንም ማወቅ ያስፈልግዎታል። ዋናዎቹ፡ ናቸው።
- ዲያጎንሎች እርስ በርሳቸው እኩል ናቸው እና የመገናኛ ነጥቡ በግማሽ የተከፈለ ነው።
- ሲያቋርጡ ቀኝ ማዕዘኖች ይመሰርታሉ።
- ካሬውን ወደ እኩል ትሪያንግሎች ይከፋፍሉት።
ማጠቃለያ
የካሬውን ዲያግራኖች እንዴት እንደሚቆጥሩ ጥያቄው ብዙውን ጊዜ በትምህርት ቤት ውስጥ ይህንን ርዕስ ባጡ ተማሪዎች ይጠየቃል። ይሁን እንጂ ሁሉም ሰው እንደነዚህ ያሉትን የሂሳብ መሠረታዊ ደንቦች ማወቅ አለበት! በተቻለ ፍጥነት መፍታት የሚፈለግ ነው, እና ይህ የአህጽሮት ቀመሮችን እውቀት ይጠይቃል. ይህ ሁሉ እጅግ በጣም ቀላል እና ቀላል ነው, ግንበተመሳሳይ ጊዜ ለወደፊቱ በጣም ውስብስብ ችግሮችን ለመፍታት አስፈላጊው መሠረት ነው. እና የዚህ መሰረት አስፈላጊ አካል ካሬው ነው።






